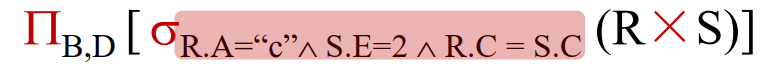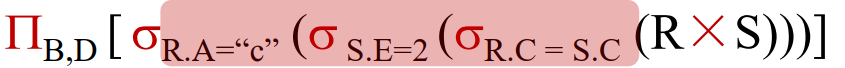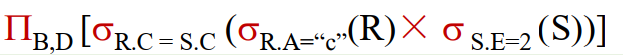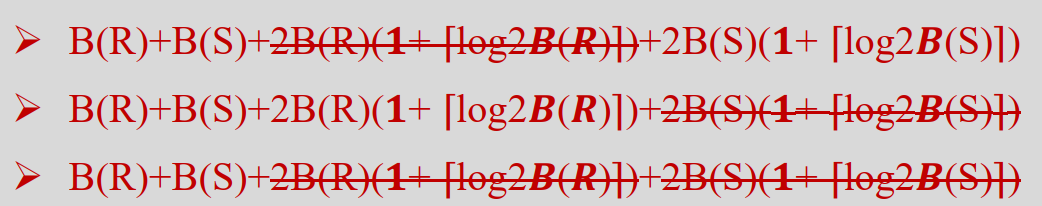第六章 查询处理和优化
第六章 查询处理和优化
主要内容:理解常用数据库物理层执行模型;物理层执行过程的数据访问方法;核心逻辑算子的物理执行算法。
- 基本要求
a)理解常用数据库物理层执行模型
b)熟悉数据库物理层对各逻辑算子的具体执行算法
c)掌握同种逻辑算子多种物理实现策略的异同和适合的场景
- 重点、难点
重点: 数据库物理层对各逻辑算子的具体执行算法
难点: 掌握同种逻辑算子多种物理实现策略的异同和适合的场景
主要内容:数据库SQL引擎中的编译过程,统计信息获取,查询优化(包括基于代价的优化和基于规则的优化)。
- 基本要求
a)了解SQL编译过程中的抽象语法树生成
b)熟悉查询优化的基本步骤
c)掌握基于规则的优化和基于代价的优化的区别和联系
d)掌握基于代价的优化和数据库统计信息间的关系
e)熟悉查询优化过程中连接顺序剪枝和过滤算法
- 重点、难点
重点: 查询优化的基本步骤
难点: 基于代价的优化及连接顺序剪枝算法。

查询优化,一般从逻辑和物理两个层面进行。逻辑层面优化的目标是找出与原始查询等价但更加高效的关系代数表达式,主要是通过调整关系代数运算顺序来使每步运算要处理的数据行数最少。例如数据库一般会将选择运算下推,以尽早缩减参与运算的数据行数。逻辑优化后需要进行物理优化,主要是利用数据库的数据规模(如数据块大小和统计信息等)来估计计划执行的代价,并从众多候选计划中 出代价最小的计划。物理优化需要选择每个算子的物理实现算法,例如在连接操作中选择嵌套循环连接或哈希连接,并确定多表连接时的连接顺序。查询优化使数据库尽量选择较为高效的执行方案,从而提高数据库执行查询的效率。与逻辑优化不同的是,物理优化过程需要考虑关系实例的统计信息特征,例如一列非重复值的数量,以准确计算不同物理操作的执行代价。

一、查询解析
词法分析

将输入的SQL语句拆解为单词(token)序列,并对不同类别的单词进行分类标记,形成字符标记流。
正则表达式:➢ 标识符ID [a-z][a-z0-9]+
➢关键词 Keyword select | from | where
➢分隔符 SEP , | ;
➢运算符 OP = | + | <
➢ INT [0-9]+
有限状态自动机

语法分析
移进:将字符标记放入栈中
归约:用非终结符代替栈的顶部元素 出栈 并在AST中新建对应的语法类节点
语义分析
检查关系(表名)、属性(列名)、数据类型.......
授权检查
将语法分析树转换为查询树
二、逻辑重写
声明式的SQL->查询执行的逻辑顺序
基于规则的优化(Rule-based Optimization, RBO)
➢ 查询的逻辑重写,以尽可能减少不合理的开销
➢ 基于(关系代数的等价变换) 规则
➢ 调整操作顺序
➢ 生成:由逻辑运算符组成的逻辑计划(树)
➢ 逻辑运算符:关系代数的算子(π , σ , ⋈, …)
➢ 与关系实例无关
RBO通用规则:
-
复合谓词拆分
-
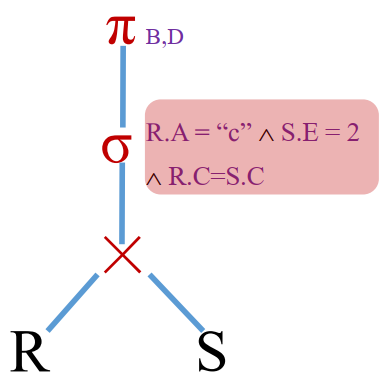
谓词下推
-
笛卡尔积改为连接
-
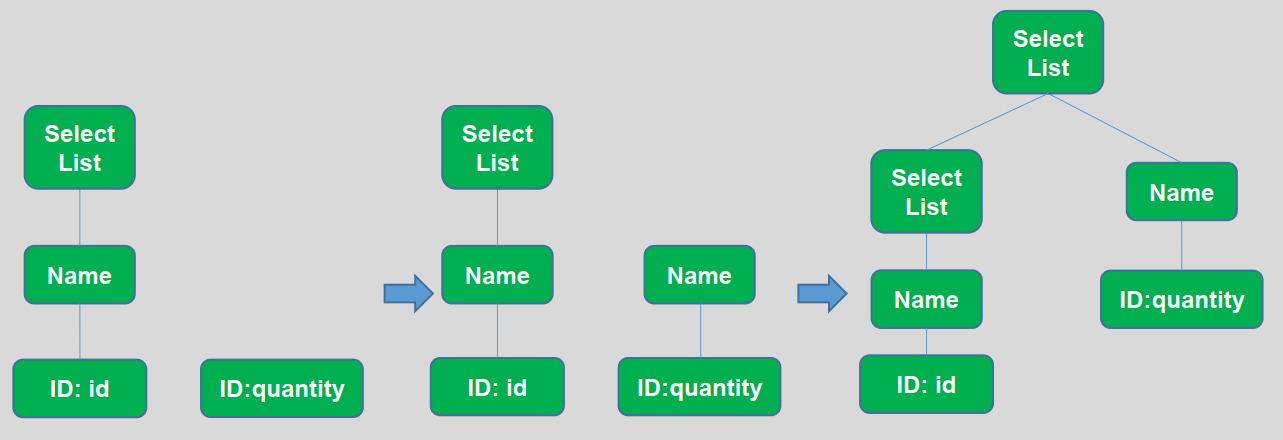
投影下推 :先过滤掉不必要的列,只携带必需的列进行计算和传递
-
嵌套查询
重写(为连接查询)【 ref., 视图消解】
实体化临时表【 ref., 实体化视图】
-
表达式重写
三、物理算子
算子:选择、连接、排序、聚集等
基于代价的优化(Cost-based Optimization, CBO)
➢ 查询的物理优化
➢ 使用代价模型,对操作进行代价估计
➢ 衡量所有可能的执行方式,选择执行代价最小的
➢ 生成:由物理操作符组成的物理执行计划(树)
➢ 物理操作符:关系代数算子的具体物理实现 (1 -> n映射)
➢ 与关系实例相关
➢ 需要使用实例的统计信息
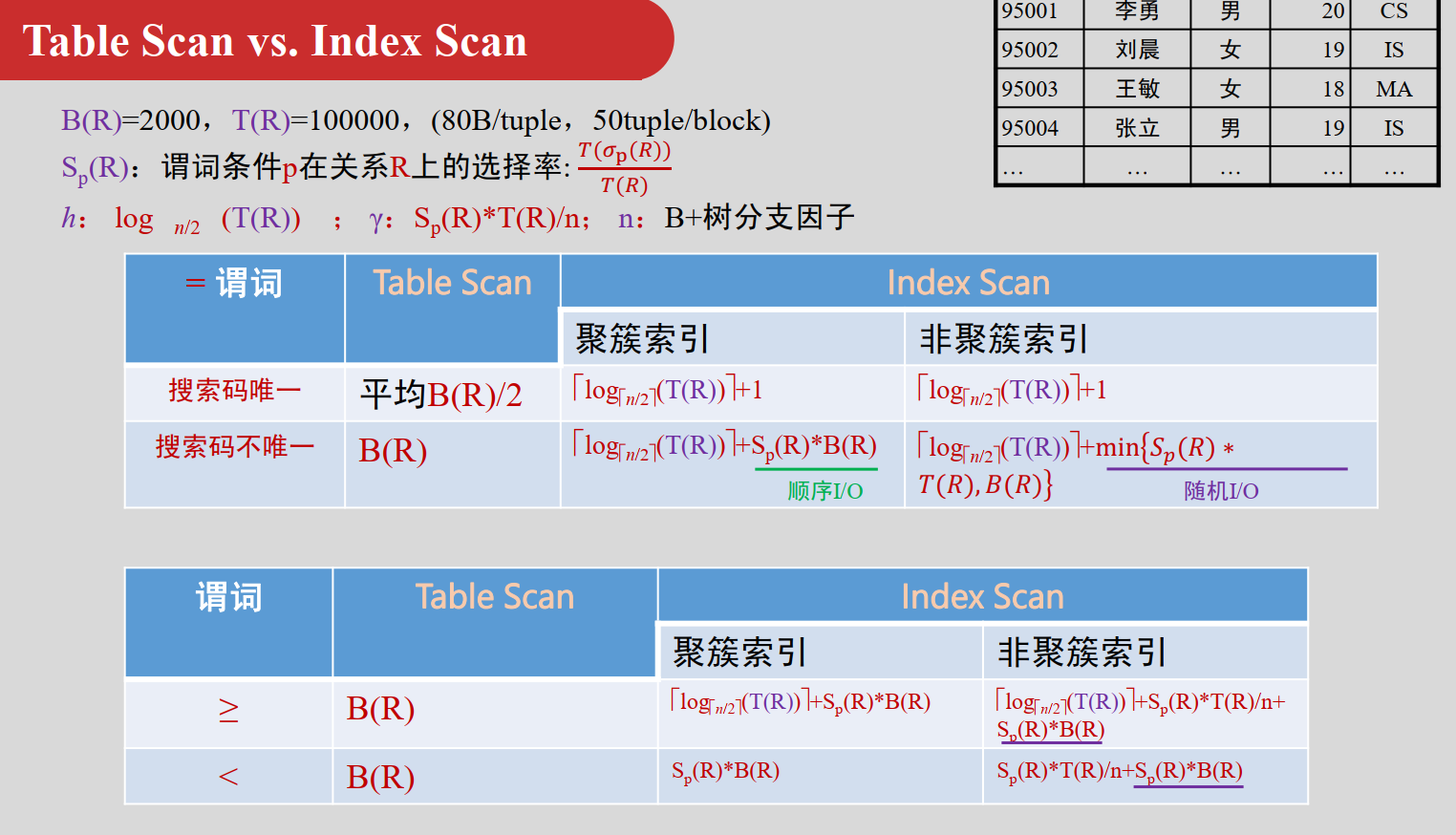
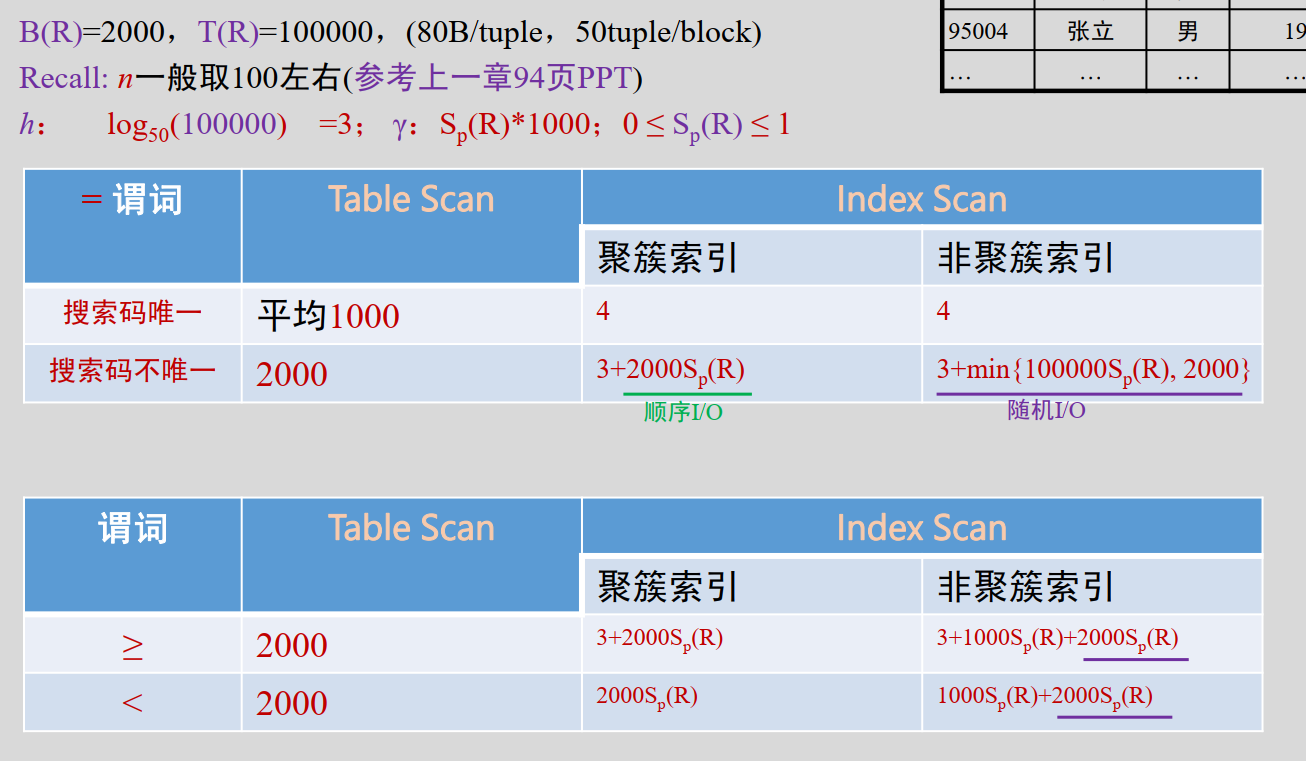
设B(R)为关系R的块(页)数, T(R)为关系R中的元组数
例如B(R)=2000, T(R)=100000, (80B/tuple)
选择σ
全表扫描 Table Scan
顺序扫描整个Table,依次检查每个元组以衡量是否满足过滤谓词
➢ 等值谓词 “ = ”
- 对应属性是码/唯一约束(只有一个)时,命中即可结束,平均B(R)/2
- 代价是B(R)
- 最多B(R)次I/O操作
➢比较谓词 “ <, >, ≤, ≥ ”
- B(R)次I/O操作
索引扫描 Index Scan
借助索引的扫描(索引->Table),设树深为 (每访问一个内部节点都会进行一次I/O操作)
过滤谓词必须是某个索引的搜索码
➢ 等值谓词 “ = ”
-
聚簇索引(元组按搜索码顺序存储在连续的块中)
搜索码唯一 ,命中一个即结束 h+1次I/O
(还有的一次是读取目标元组所在的磁盘块)搜索码不唯一 ,会命中多条记录,多条记录存储于连续块 h+b次I/O
根据 𝑏 / 𝐵(𝑅) = 𝑇(𝜎p(𝑅)) / 𝑇(𝑅)
该记录分布到的块数𝑏 = 𝐵(𝑅) × 𝑇(𝜎p(𝑅)) / 𝑇(𝑅) -
非聚簇索引
搜索码唯一 ,命中一个即结束 h+1次I/O
搜索码不唯一 ,定位到的记录分布于相对随机的 𝑏′ 个磁盘块, h+ b′ 次I/O
𝑏′ = 𝐵 (𝜎𝑝(𝑅)) = min{ 𝑇(𝜎p(𝑅)) , B(R) } 这里是代价,故作最坏打算
➢ 比较谓词 “ ≥v ”
- 聚簇索引
先定位到v对应的叶子结点,然后从其指向的数据块顺序扫描所有剩余块(b块)
h+b = h + B(R) * T(σA≥v(R)) / T(R)
选择率 = T(σA≥v(R)) / T(R) - 非聚簇索引
先定位到v对应的叶子(h次),然后向后顺序扫描剩余(γ个)叶子提取所有指向记录的指针,根据获取的指针读取对应数据块(随机I/O T(σA≥v(R)))
h + γ + T(σA≥v(R))
γ = T(σA≥v(R)) / n
n是B+树因子,每个叶子节点包含 n 个指针。满足条件的指针数为 T(σA≥v(R))
➢ 比较谓词 “ <v ”
- 聚簇索引
直接顺序扫描数据块,直到v (无需定位到v对应的叶子,数据块中存储的数据行按照聚簇索引的顺序排列,不使用索引 )
B(R) * T(σA<v(R)) / T(R) - 非聚簇索引
直接顺序扫描索引的叶子提取所有指向记录的指针,直到包含v的叶子(γ个),根据获取的指针读取对应数据块(随机I/O T(σA≥v(R)))
γ + T(σA<v(R))

索引扫描与仅索引扫描的区别:索引扫描需要额外访问表以取得非索引列,而仅索引扫描则完全依赖索引,不访问表数据。
- 索引扫描(Index Scan):
- 索引扫描需要访问索引来确定哪些行符合查询条件。
- 从索引获取到行的指针后,它需要回到数据表中以取得完整的行数据。
- 适用于索引覆盖一部分查询条件的情况,需要访问表数据以获取不在索引中的列。
- 仅索引扫描(Index-Only Scan):
- 当查询所需的数据完全被索引覆盖时,可以使用仅索引扫描,这时不必访问数据表。
- 这种扫描提供更高的性能,因为它避免了对表的访问,仅仅通过索引即可获取所有需要的数据列。
- 当查询的列已经全部在索引中时用此方法,减少了对表的I/O访问。
全表扫描VS索引扫描
- 全表扫描:适合小表和需要处理大部分或全部数据的查询。
- 聚簇索引扫描:适合精确匹配和顺序访问大量记录的查询。
- 非聚簇索引扫描:适合精确查询和部分范围查询,但由于数据可能分布在不同块中,随机I/O开销较大。
等值谓词且搜索码唯一,索引扫描好
等值谓词且搜索码不唯一 and 比较谓词,聚簇索引扫描好;全表扫描和非聚簇索引扫描谁好要看选择率,选择率高可能全表扫描相对好,选择率低可能非聚簇索引扫描相对好,
排序τ
外归并排序
基于外存,适用于排序无法完全放入内存的大型数据集。
它通过分阶段的处理,将数据分块排序并逐步归并,最终得到有序的数据
归并段( run)
- 一个键/值( Key/Value )列表
- Key:用于排序的属性列
- Value:元组ID/元组内容
以2路为例
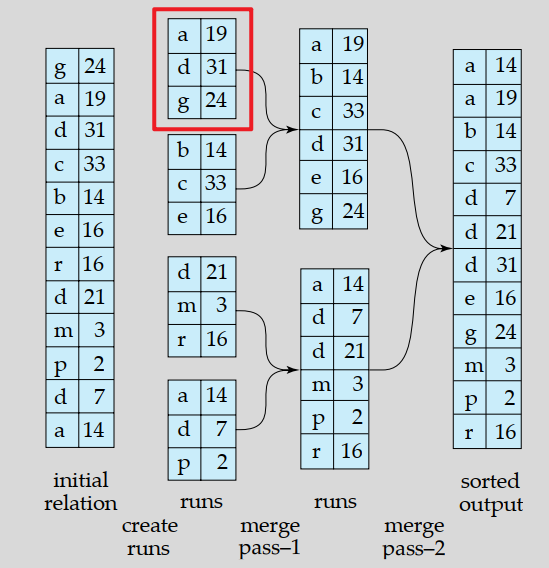
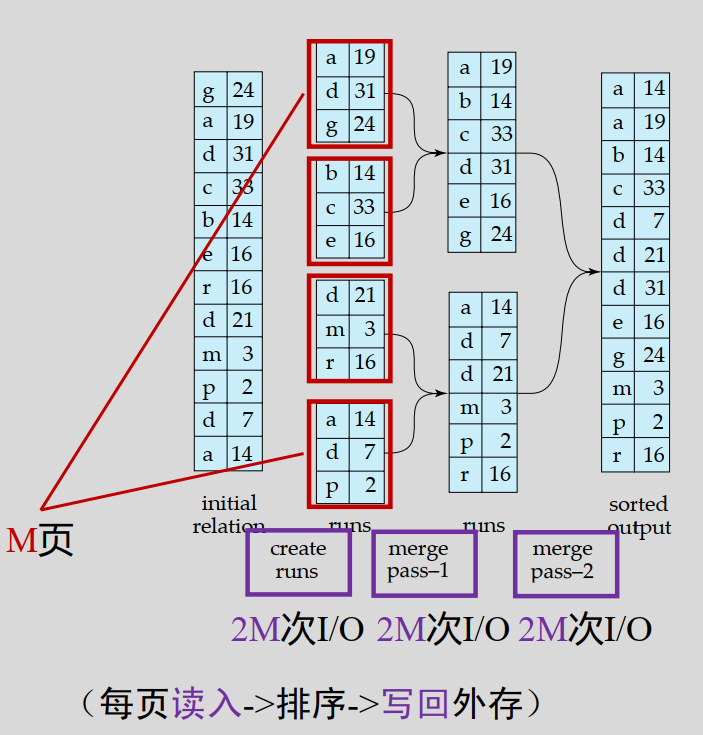
➢初始分块排序:将大数据集分成适合内存的M块,依次读入M个块(完整的用于排序的K/V列表共占M页),在内存中进行排序,将排序后的数据块写回到磁盘,形成有序的子文件(runs)
➢归并排序:从磁盘读取两个有序的子文件合并,生成更大的有序子文件,写回磁盘。上述过程使用缓冲池中的3个帧(2个用于输入、一个输出)
重复合并过程,直到所有子文件合并成一个最终的有序输出文件。
I/O数量:
- 趟数(树高):1 + ⌈log2M⌉
- 每趟: 2M
- 合计: 2B(R) × (1 + ⌈log2B(R)⌉)
连接⋈
SELECT R.StuID, S.Cno, S.grade FROM Student R, SC S WHERE age = 19 AND R.StuID=S.Sno;
嵌套循环 Nested Loop Join
➢扫描外表(左表)
➢ 对于外表的每个符合条件的记录,根据连接条件,扫描内表(右表)来执行连接。
1 | for each tuple i in R: |
左表的每一行都想扫一遍右表
I/O数量:
- 外层循环: B(R)
- 内层循环: T(R)*B(S) (左表的每一行都想扫一遍右表)
- 合计: B(R)+T(R)*B(S)
根据不对称产生思考,能否R与S互换,即左右表互换。结论:小表做外表(左表) 这样扫一整遍右表的次数少了
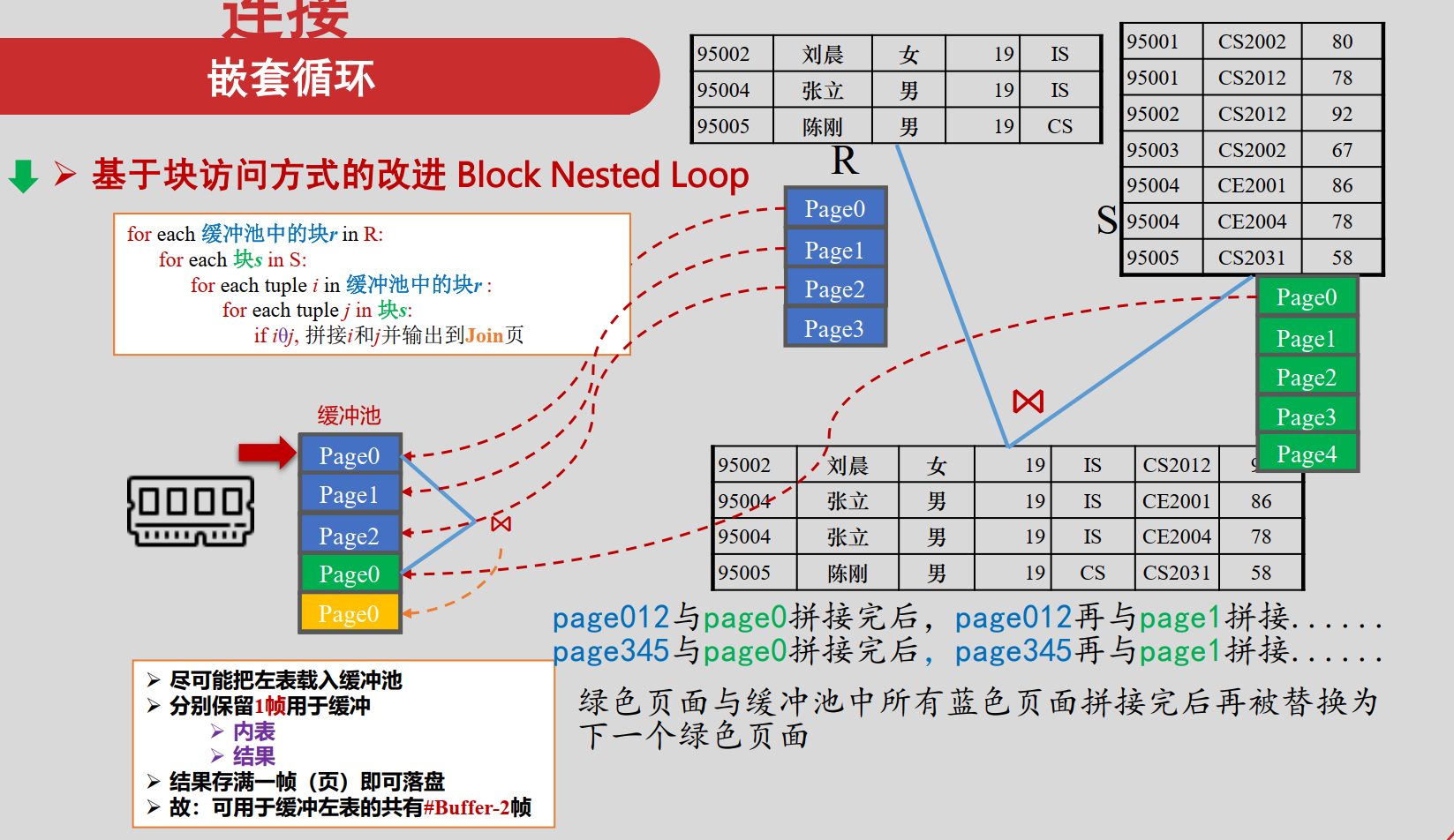
基于块访问方式的改进 Block Nested Loop Join
j借助缓冲池,将外表的块读入内存,然后对每个块中的每个元组,与内表的所有元组进行比较。
1 | for each 块r in R: |
尽可能把左表载入缓冲池
分别保留1帧用于缓冲内表和结果,故可用于缓冲左表的共有(#Buffer - 2)帧
结果存满一帧(页)即可落盘
缓冲内表的那一帧主动拼接当时缓冲池所含所有的外表页面
I/O数量:
- 外层循环: B(R)
- 内层循环: ⌈ B(R) / (#Buffer-2) ⌉ * B(S)
- 合计: B(R) + ⌈ B(R) / (#Buffer-2) ⌉ * B(S)
- 如果#Buffer - 2 >= B(R) ,即外表能一次全部放入缓冲池, B(R) + B(S)
排序合并 Sort-Merge Join

➢排序:R,S分别按照连接码排序
如果输入关系尚未排序,对两个输入关系分别按连接属性进行排序
可以使用外部排序算法,如外归并排序(External Merge Sort),来处理不能完全放入内存的大型数据集。
➢合并:两表分别维护1个游标按顺序检查匹配
分别指向两个已排序关系的第一个元组,比较当前元组对的连接属性值。
如果两者匹配,将匹配的元组对加入结果集中,并移动两个游标到下一个元组。
如果不匹配,移动具有较小连接属性值的指针到下一个元组,继续比较。
直到至少一个关系的所有元组都被处理完。
I/O数量:
- 排序: Sort(B(R)) + Sort(B(S))
- 合并:B(R) + B(S)
- 合计: 2B(R) × (1 + ⌈log2B(R)⌉) + 2B(S) × (1 + ⌈log2B(S)⌉) + B(R) + B(S)
- 若表本身已有序则无需排序
哈希连接 Hash Join
假设两个关系 R 和 S 分别具有 N 和 M 个块,较小的关系记为R,较大的关系记为S
当数据量大到无法全部放入内存时,需要使用外部哈希连接。
➢分桶:扫描R表,在连接码上用哈希函数h将R中的元组映射到不同的桶(构造)
扫描S表,用h将S中的元组找到对应的桶,在对应的桶内进行匹配(探查)
读取R,用哈希函数h将R分区,将这些分区写回磁盘——2N次I/O
读取S,用哈希函数h将S分区,将这些分区写回磁盘——2M次I/O
➢连接:逐个读取每对分区的块,并在内存中进行哈希连接(直接输出,无需将结果写到磁盘)
读取N + M次
I/O数量:
- 分桶:2B(R) + 2S(R)
- 连接:B(R) + S(R)
- 合计:3B(R) + 3S(R)
- 若表比较小,能一次放入内存,则可以在内存中直接作哈希连接,B(R) + S(R)

嵌套循环连接VS排序合并连接VS哈希连接

范围谓词:只能用嵌套循环连接
等值谓词:
- 若R或S在连接属性上已有序:排序合并连接
- 大多数情况:哈希连接
- DBMS需要进行代价估计(依靠统计信息和代价模型)来决定实际物理操作符的选择
四、查询优化CBO
访问计划:为了执行一条SQL查询语句而将一系列访问方法和连接方法缝合在一起。
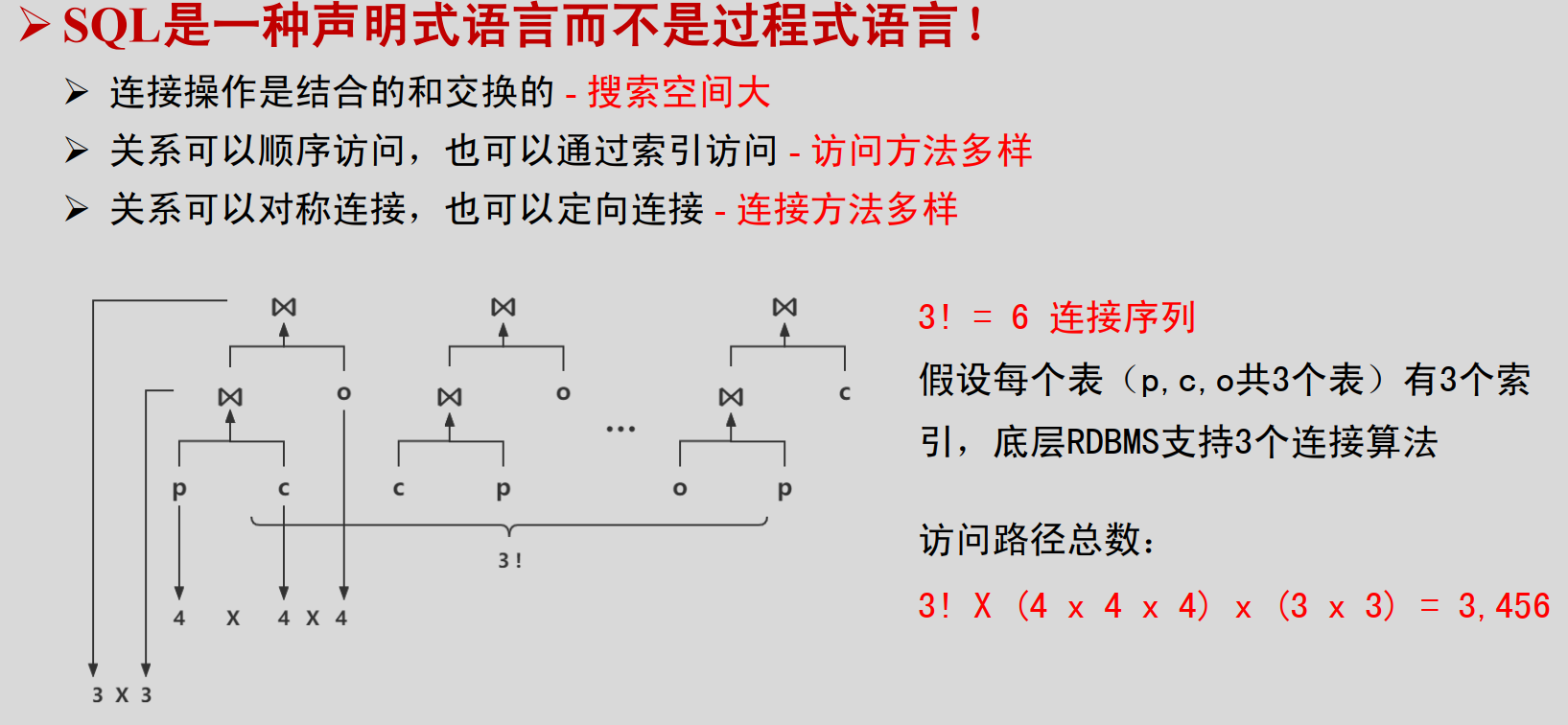
访问路径:假设底层RDBMS支持 j 个连接算法,并且每个表平均有 i 个索引,则每个表有(i+1)个访问方法(还有的那一种是顺序访问),那么n表连接访问路径总数:n! x (i + 1)n x jn-1
n!:连接顺序
(i + 1)n:每个表有(i+1)种访问方法
jn-1:两两连接的方法
SQL语言的查询优化是一个NP-Hard问题!
CBO(基于代价的优化)

访问计划枚举
- 1-复合:
- 2-复合:
- n-复合:(n-1)复合⊕1-复合 自底向上,动态规划(不一定最好)

连接顺序剪枝:通过排除不可能的或低效的组合以提高优化器效率的方法,例如将过滤后行数少的表作为驱动表(首表)进行连接
代价估算
开销模型
是DBMS用于从众多访问路径中选择执行计划的基础,用于计算
估算查询执行计划的代价,包括I/O、CPU、内存、网络等资源的消耗,这些开销与数据量密切相关
统一标准量:为了选择唯一的执行计划,需要将右侧归一为标准量,可以采用相对比例或绝对大小参考值。
需要用到基数估算和选择率估计
基数估算:使用统计信息估算 选择、连接等查询操作 返回的元组数量
基数(cardinality)是指查询结果的元组数
选择率估计:
统计信息
统计信息是关于数据分布和表结构的元数据,帮助查询优化器估算查询操作的代价。
DBMS会自动收集所有索引列以及最多k个非索引列的统计信息,在数据字典中存储
通常包括:
-
表的统计信息:
- T(R):总行数,表中记录的总数
-
列的统计信息:
-
Card(R,A):列 A 中不同值的数目
-
Null(R,A):列 A 中NULL 值的数目
-
Hist(R,A):直方图(histogram),列 A 值的分布情况。 更细粒度
-
选择率估计:
均匀分布?属性独立?
need 总行数、基数、直方图
| 查询 | 情况 | Card(R,A) | Sp(R) |
|---|---|---|---|
SELECT * FROM Student WHERE StuID = '95002'; |
唯一值且不同 | T(R) | |
SELECT * FROM Student WHERE Ssex = '男'; |
均匀分布 | 2 | |
SELECT * FROM Student WHERE Sage < 18; |
非均匀分布 | 4 | 不能简单用表示,要用直方图Hist(R,A)算范围占比 |
SELECT * FROM Student WHERE Sage < 17 AND Ssex=‘男’ |
属性独立 | ||
SELECT * FROM Student WHERE Ssex=‘男’ AND Department=‘CS’; |
属性不独立(列之间有相关性) | 不能直接相乘 |
有了选择率可以计算
统计信息的维护:
- 定期或较低负载或重大改变更新
- 主动收集 ANALYZE命令
- 基数估计:蓄水池采样(随机采样)→HyperLogLog(概率算法)
- 直方图估计:蓄水池采样(随机采样)→
- 等宽直方图:区间宽度相同
- 等深直方图:区间深度相同,每个区间数据出现的频率大致相等
统计信息的局限性:只能支持原始表 ,无法支持查询过程中的中间结果,可靠性会级联递减
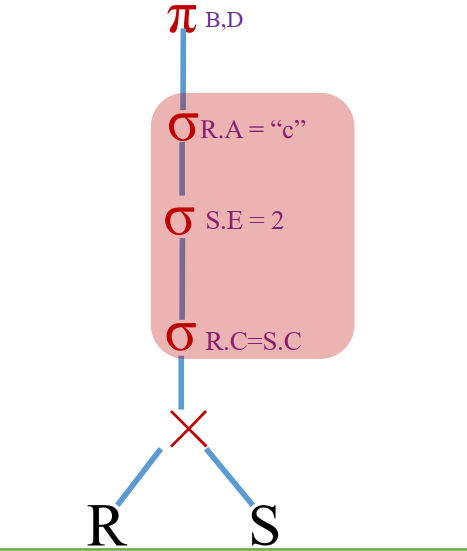
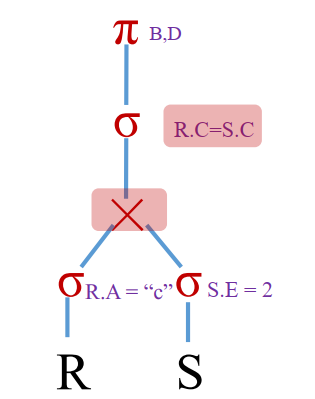
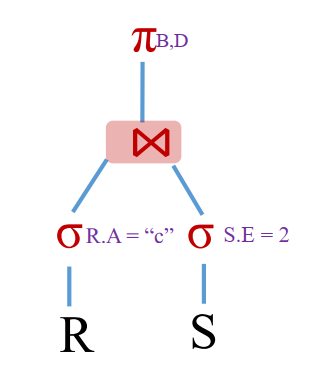
RBO-CBO案例分析

五、执行引擎
CBO输出
最优的物理计划
执行计划QEP (Query Execution Plan)
执行模型
给定QEP, DBMS执行的流程:QEP中每个物理操作符对应一段具体代码实现
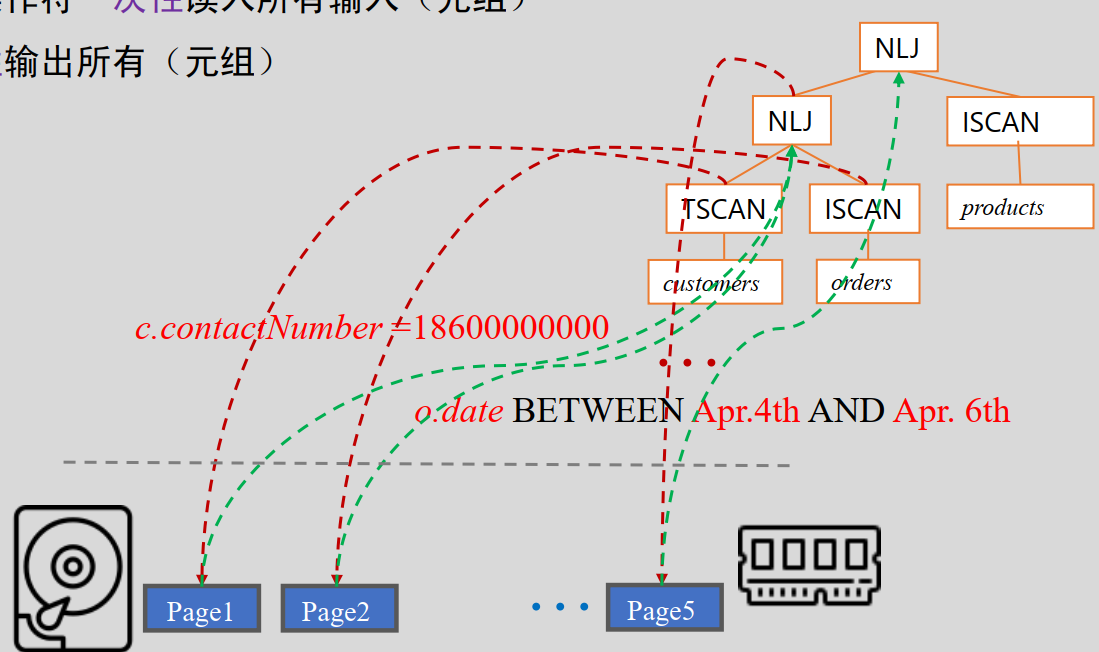
- 物化模型:每一步物理操作符的中间结果物化(甚至落盘) 后,用于下一步输入
- 每个操作符一次性读入所有输入(元组)
- 一次性输出所有(元组)
- 等每一步的结果完全弄好才能进行下一步
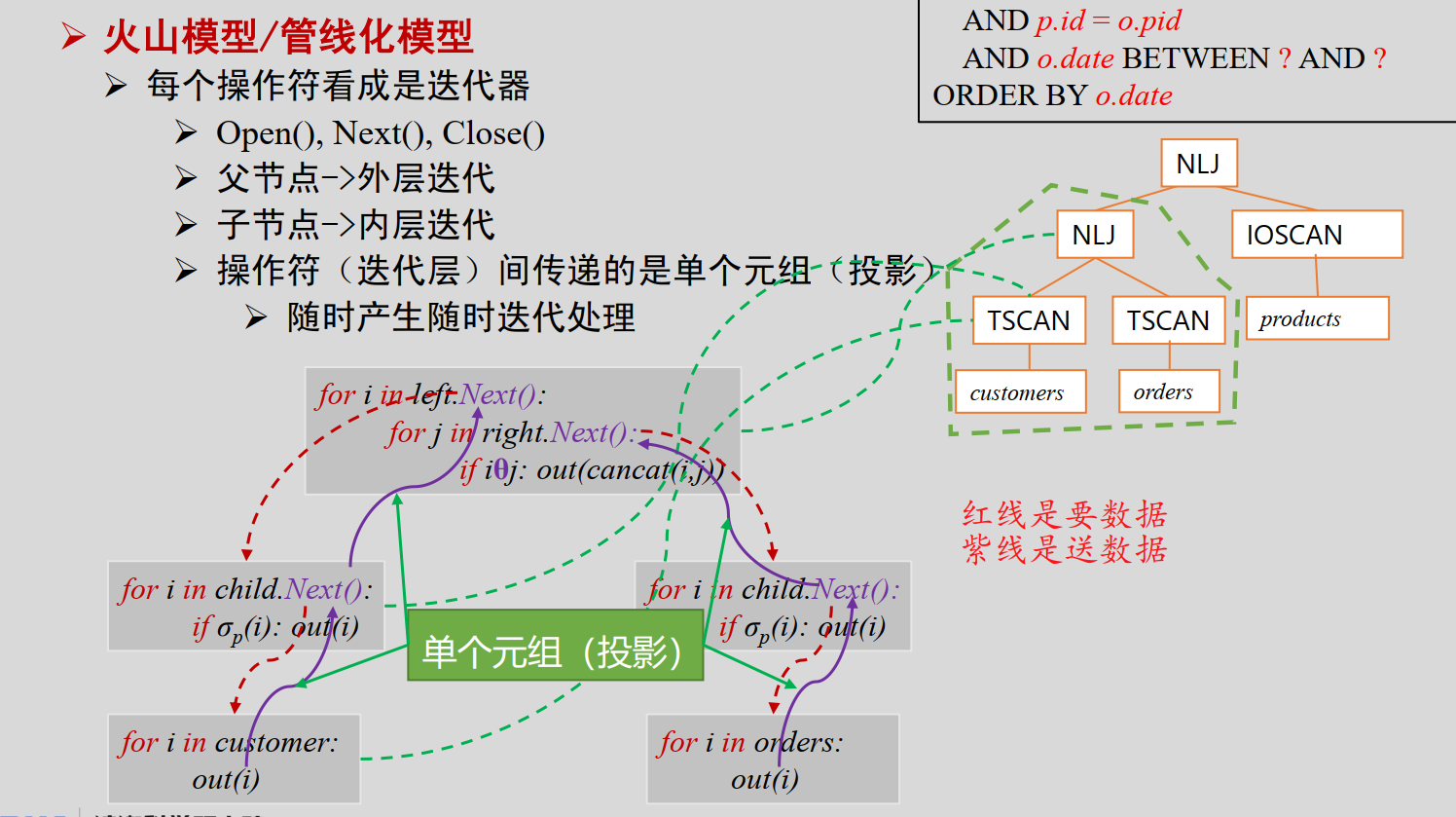
- 火山模型 :物理操作符的结果元组直接发送给下一个操作符使用(每个操作符需要实现一个Next()方法),中间不需物化
- 每个操作符看成是迭代器,父节点->外层迭代 子节点->内层迭代
- 操作符(迭代层)间传递的是单个元组(投影)
- 有一个产生就可以开始迭代处理了(像火山一样往上冒)
- 优点是减少了存储开销和I/O操作,提高了执行效率。
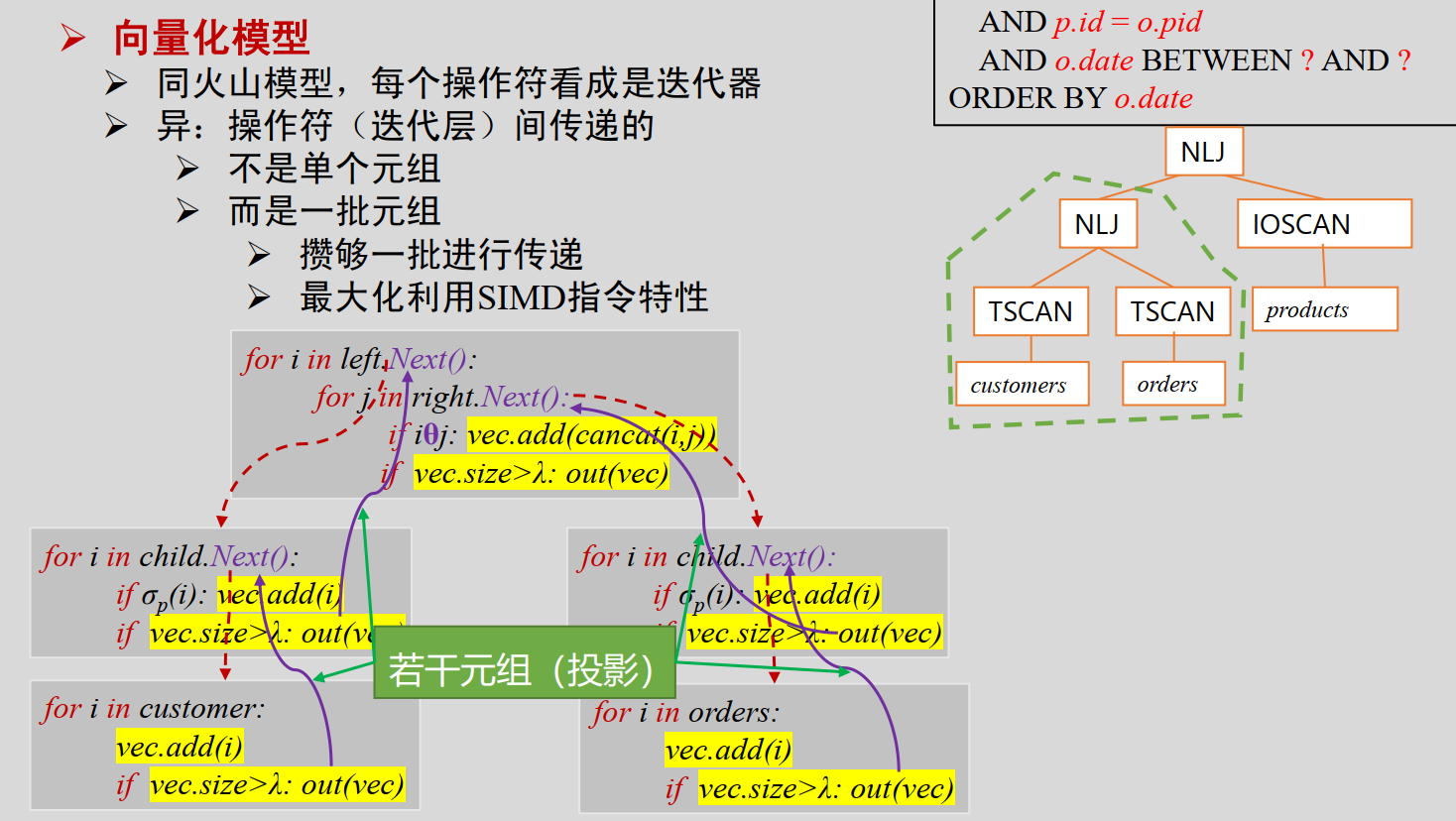
- 向量化模型:类似火山模型,但传递的不是单个元组,而是一批元组
- 一个向量内含多组内容
- 以更好的利用现代CPU的SIMD指令 (单指令多数据流)
《数据库原理》课程笔记: